什么是哈夫曼树？

哈夫曼树（Huffman Tree）是一种用于数据压缩的树形数据结构，由David A. Huffman在1952年发明。哈夫曼树通常用于无损数据压缩中，将出现频率高的字符编码成较短的二进制序列，从而减少数据的存储空间。

哈夫曼树的构建过程是基于贪心算法，即每次选择出现频率最低的两个节点合并为一个新的节点，并将它们的权值相加作为新节点的权值，直到最终只剩下一个节点为止。在构建过程中，需要保证所有节点的左子树的权值总和小于右子树的权值总和。

最终生成的哈夫曼树是一棵带权路径长度最小的二叉树，可以根据哈夫曼树来生成每个字符的编码，从而实现数据压缩。

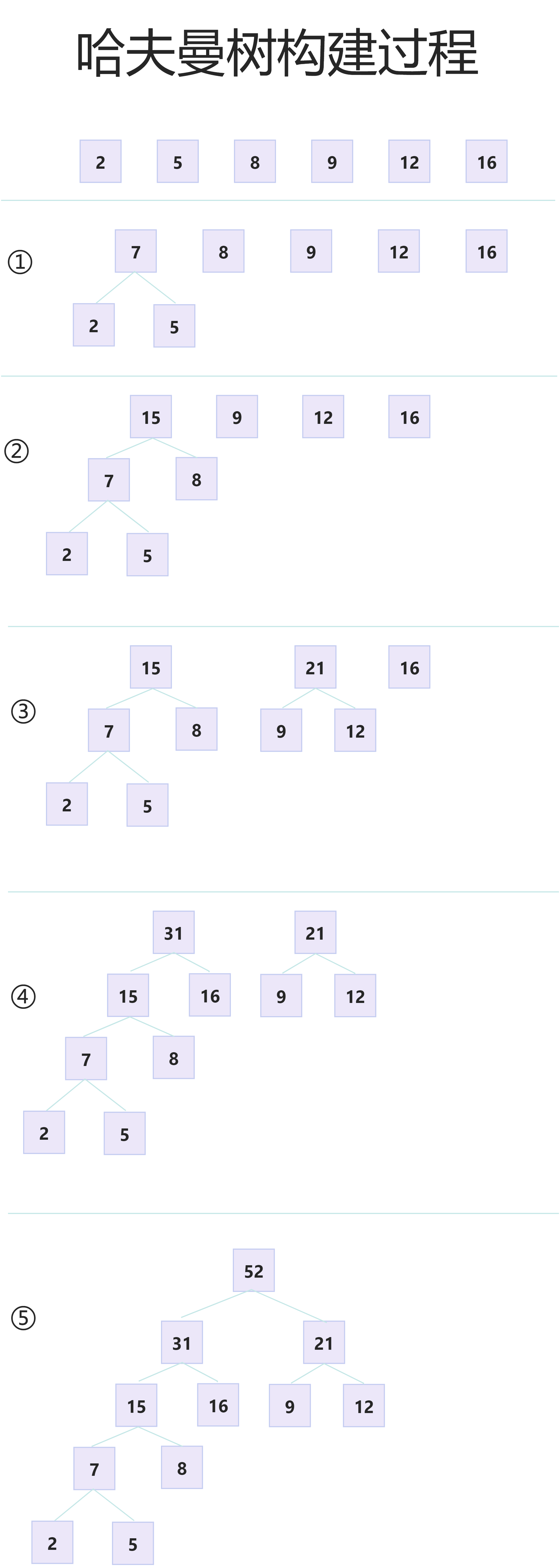
哈夫曼树构建过程

从数组中选择权值最小的两个结点，作为子结点，生成一棵树。

他们父结点的权值是他们两结点的权值之和。

然后再以此类推，重复两步，当数组中只剩下一棵树的时候，就已经构建好哈夫曼树了。

构建哈夫曼树代码（C++）

下面是使用c++实现的构建哈夫曼树的代码

//哈夫曼树构建
BTreeNode *CreateHuffman(ElemType a[],int n) {
    BTreeNode **b,*q;
    b=new BTreeNode*[n];
    int i,j;
    for(i=0; i<n; i++) {
        b[i]=new BTreeNode;
        b[i]->data=a[i];
        b[i]->left=b[i]->right=NULL;
    }
    for(i=1; i<n; i++) {
        int k1=-1,k2;
        for(j=0; j<n; j++) {
            if(b[j]!=NULL&&k1==-1) {
                k1=j;
                continue;
            }
            if(b[j]!=NULL) {
                k2=j;
                break;
            }
        }
        for(j=k2; j<n; j++) {
            if(b[j]!=NULL) {
                if(b[j]->data.weight<b[k1]->data.weight) {
                    k2=k1;
                    k1=j;
                } else if(b[j]->data.weight<b[k2]->data.weight) {
                    k2=j;
                }
            }
        }
        q=new BTreeNode;
        q->data.weight=b[k1]->data.weight+b[k2]->data.weight;
        q->left=b[k1];
        q->right=b[k2];
        b[k1]=q;
        b[k2]=NULL;
    }
    delete []b;
    return q;
}

哈夫曼前中后、层次遍历

这里和二叉树是一样的，就不过多赘述了。都是采用了递归的算法。

c++实现：

//前序遍历
void PreOrder(BTreeNode* BT) {
    if(BT==NULL){
        return;
    }
    cout<<BT->data.letter<<' ';        
    PreOrder(BT->left);
    PreOrder(BT->right);
}
//中序遍历
void InOrder(BTreeNode* BT) {
    if(BT==NULL){
        return;
    }
    InOrder(BT->left);
    cout<<BT->data.letter<<' ';        
    InOrder(BT->right);
}
//后序遍历
void PostOrder(BTreeNode* BT) {
    if(BT==NULL){
        return;
    }
    PostOrder(BT->left);
    PostOrder(BT->right);
    cout<<BT->data.letter<<' ';        
}

层次遍历：

需要使用队列，首先根节点入队列，只要队列不是空的时候，头结点出队，并且访问出队结点，然后出队结点的左右孩子结点入队列。

一直重复上述步骤，最终即可实现层次遍历。

//层次遍历
void LevelOrder(BTreeNode* BT) {
    const int MaxSize=30;
    BTreeNode* q[MaxSize];
    int front=0,rear=0;
    BTreeNode* p;
    if(BT!=NULL) {
        rear = (rear+1)%MaxSize;
        q[rear] = BT;
    }
    while(front!=rear) {
        front=(front+1)%MaxSize;
        p=q[front];
            cout<<p->data<<' ';
        if(p->left!=NULL) {
            rear=(rear+1)%MaxSize;
            q[rear]=p->left;
        }
        if(p->right!=NULL) {
            rear=(rear+1)%MaxSize;
            q[rear]=p->right;
        }
    }
}

哈夫曼树编码

很多时候，再通讯的时候会使用到，需要对信息进行编码，这个时候哈夫曼树就可以对这些通讯实现最优的编码。

下面是哈夫曼树编码的实现算法：

通过递归调用实现哈夫曼编码，函数首先判断当前结点是否由孩子结点，如果没有孩子结点，就直接遍历静态数组，输出，此时数组就是当前结点的哈夫曼编码。如果有孩子结点，就继续递归，左孩子结点就给数组赋值为0，右孩子结点就给结点赋值为1。

c++:

//哈夫曼树编码，len传入的时候是0，因为根节点的是0
void HuffManCoding(BTreeNode *FBT,int len){
    static int a[10];
    if(FBT!=NULL){
        if(FBT->left==NULL&&FBT->right==NULL){            //这里证明已经到了叶子结点，可以开始将a数组进行遍历输出即可形成编码
            cout<<FBT->data.letter<<"的编码为：";
            for(int i=0;i<len;i++){
                cout<<a[i];
            }
            cout<<endl;
        }else{                        //还不是叶子结点，递归调用继续往下走
            a[len]=0;
            HuffManCoding(FBT->left,len+1);
            a[len]=1;
            HuffManCoding(FBT->right,len+1);
        }
    }
}