07— 最大子数组和【LeetCode 53】

题目

53. 最大子数组和 - 力扣（LeetCode）

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例2：

输入：nums = [1]
输出：1

示例3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104

解题

解法一

思路

思路，通过动态规划的思路可以解决该问题。

由于题目中要求求出最大的连续的子数组，因此可以通过动态规划，来判断当前轮到的数，是否应该成为一个新的连续子数组的开头。

需要定义一个dp[i]数组，dp[i]中存储的数据：

dp[i] = max(num[i],dp[i-1]+nums[i])

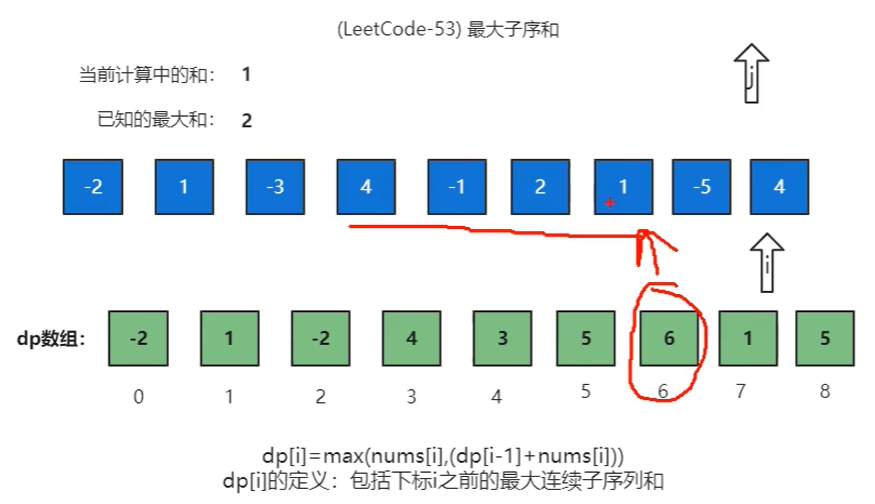
意思就是dp[i]存储的是nums[i]是否作为一个新的开始，要是之前的数+num[i]的数还小于num[i]，就表明，num[i]适合作为一个新的子数组的起始。

最后只需要从dp[]中找到最大的值，就是最大连续子数组的值。

解决

public int maxSubArray(int[] nums) {
        int length = nums.length;
        //dp数组
        int[] dp = new int[length];
        int result = Integer.MIN_VALUE;
        //初始化dp，第一个数值默认为数组第一个值
        dp[0] = nums[0];
        //遍历填充dp
        for(int i=1;i<length;i++) {
            dp[i] = Math.max(nums[i],dp[i-1]+nums[i]);
        }
        //开始寻找dp中最大的值，就是最大连续子序列
        for(int i=0;i<length;i++){
            if(result<dp[i]) {
                result = dp[i];
            }
        }
        return  result;
    }

结果

> 2023/07/15 18:17:56    
解答成功:
    执行耗时:2 ms,击败了44.11% 的Java用户
    内存消耗:56.3 MB,击败了38.07% 的Java用户

解法一优化

得出最后结果是用了时间2ms。

耗时的原因是因为用了数组存储dp，然后又需要从dp数组中进行遍历找最大值，因此消耗了较多的时间。

然后就寻思用两个变量来替代数组，因为其实我发现有用的记录变量只有两个，一个是前面的连续的最大值，一个是结果，只需要定义这两个结果，然后不断更新这两个变量，完全可以将时间复杂度更大的数组存储的方式替换掉。

class Solution {
    public int maxSubArray(int[] nums) {
        int length = nums.length;
        //刚开始默认的最大连续子集为第一个nums[0]
        int result = nums[0];
        //一开始连续的默认值为nums[0]
        int temp = nums[0];
        //遍历填充dp
        for(int i=1;i<length;i++) {
            temp = Math.max(nums[i],temp+nums[i]);
            result = Math.max(result,temp);
        }
        return  result;
    }
}

优化结果：

> 2023/07/15 18:28:36    
解答成功:
    执行耗时:1 ms,击败了100.00% 的Java用户
    内存消耗:58.1 MB,击败了13.02% 的Java用户